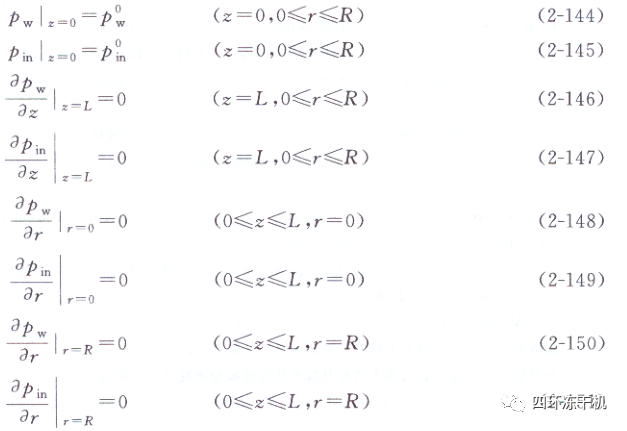通常流體的擴散滿足Fick定律,固相中的擴散也常常沿襲出流體擴散過程的處理方法。但分形多孔介質中非均勻孔隙的復雜性,若仍沿用傳統方法描述���,將與實際情況相差太大�����。
根據文獻可知�,若用ρ(r��,t)表示擴散概率密度,在d維歐氏空間的一般擴散方程具有如下形式:
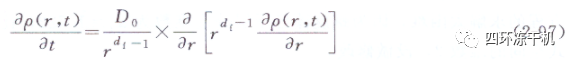
若用M(r����,t)表示時刻t�����,在r + dr之間的球殼中的擴散概率,用N(r�,t)表示總的徑向概率�,也表示單位時間流過的物質流量�����,即通量���。則概率守恒的連續方程可寫為:

在分形介質中:

根據Fick擴散定律,在d維歐氏空間中���,物質流與概率流之間滿足如下關系:
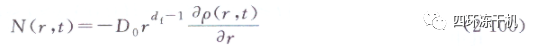
把式(2-100)中擴散系數D0用分形介質中的擴散系數代替���!Ddf(r),空間維數d用分形維數代替,從而給出了分形介質中質量流量與概率密度之間類似的關系式:
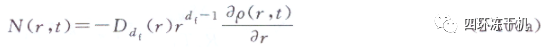
把式(2-98)和式(2-100a)代人式(2-97)中���,可得分形介質中的擴散方程:
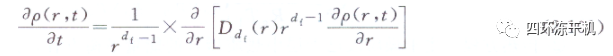
比較式(2-97)和式(2-101)��,可以看出���,分形介質中擴散方程和歐式空間擴散方程的區別在于���,空間維數d用分形維數代替�,擴散系數用分形多孔介質中的擴散系數�����,由于分形介質中的擴散系數不是常數�����,與擴散距離有關�����,擴散系數不能提到偏微分號外邊。
把式(2-96)代人式(2-101)中��,可得分形多孔介質中的擴散方程為:
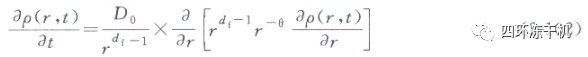
2.2.3.5凍干模型的建立
模擬螺旋藻在如圖2-23所示的小盤中的凍干過程��,在建立熱質耦合平衡方程時做了如下假設:
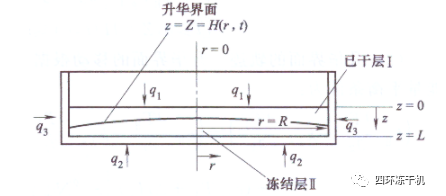
① 升華界面厚度被認為是無窮?�。?/span>
② 假設只有水蒸氣和惰性氣體兩種混合物流過已干層��;
③ 在升華界面處����,水蒸氣的分壓和冰相平衡;
④ 在已干層中氣相和固相處于熱平衡狀態,且分形對傳熱的影響忽略不計;
⑤ 凍結區被認為是均質的����,熱導率、密度��、比熱容均為常數�����,溶解氣體忽略不計�����;
⑥ 物料尺寸的變化忽略不計�����。
下面所建的數學模型是在1998年Sheehan 建立的二維軸對稱模型基礎上建立的��,只是水蒸氣和惰性氣體的質量流量根據分形多孔介質中的擴散方程進行修改,在修改的過程中將擴散系數改為分形多孔介質中的擴散系數,考慮到若將歐式空間的維數改為分形維數��,方程的求解太困難����,因為螺旋藻已干層分形維數為df= 1.7222�����,比較接近2��, 所以仍沿用歐式空間的維數2����,沒做修改�。
(1)主干燥階段數學模型
①傳質方程。已干層分形多孔介質中的傳質連續方程如下:
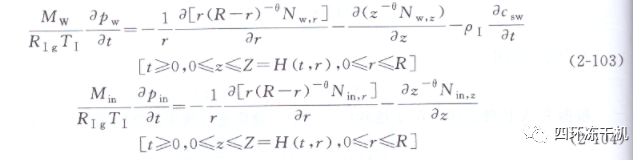
其中
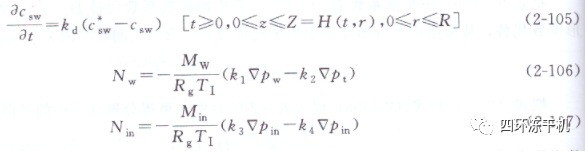
②傳熱方程。主干燥階段已干層中熱質耦合的能量平衡方程,其中傳質相與分形指數有關:
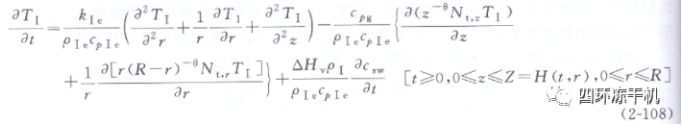
凍結層中能量平衡方程:
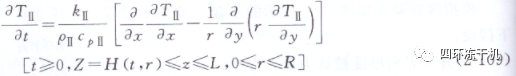
(2)升華界面的軌跡 升華界面的移動根據升華界面處的熱質耦合能量平衡的條件確定, 能量平衡條件為:
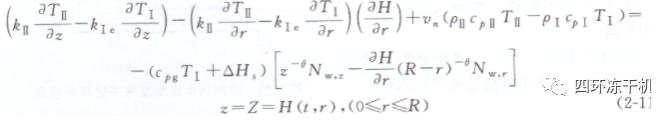
其中

(3)二次干燥階段數學模型 傳熱能量平衡和傳質連續方程:
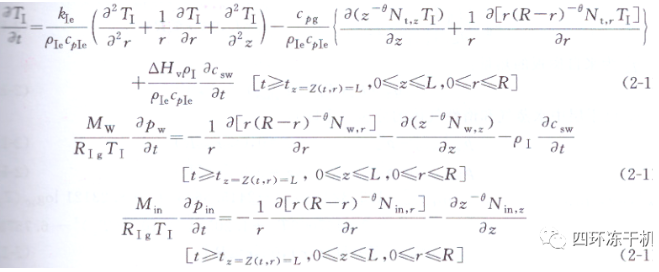
結合水的移除用方程(2-115)表示:

2.2.3.6初始條件和邊界條件
(1)主干燥階段初始條件和邊界條件也就是方程(2-103)~方程(2-109)的初始條件和邊界條件���。
①初始條件。當t=0時����,
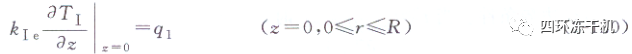
②邊界條件���。當t>0時:
a.已干層(I區)的溫度:
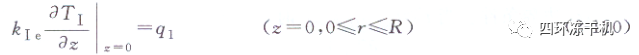
q1為來自已干層頂部的熱量
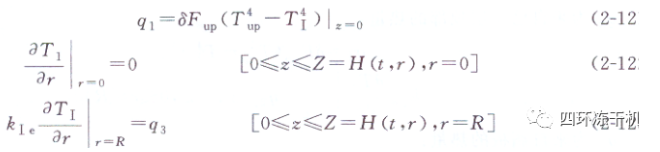
q3為來自瓶壁的熱,通過下式確定:

b.凍結層(Ⅱ區)的溫度:
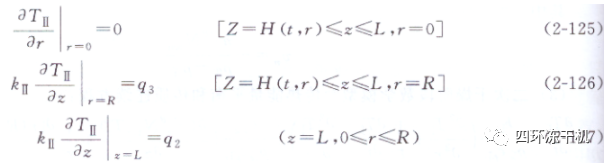
q2為來自擱板的熱量:

c.已干層中水蒸氣和惰性氣體的分壓(I區):
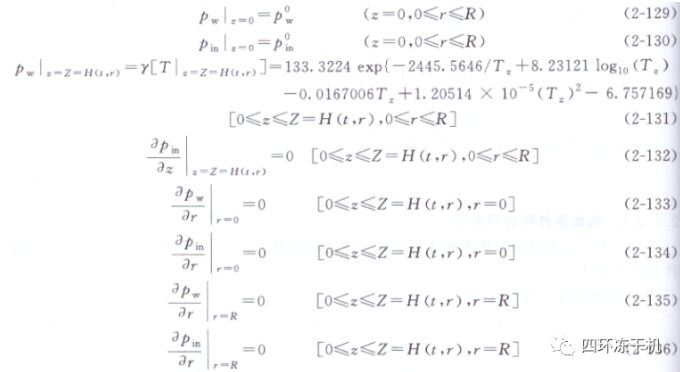
(2)二次干燥階段初始條件和邊界條件 也就是式(2-60)~式(2-63)的初始條件和邊界條件�。
①初始條件。式(2-112)~式(2-115) 的初始條件是主干燥階段結束時的條件,即t=tz=z(t,r)=L時表示移動界面消失時的條件,通常情況也代表二次階段的開始�����。
②邊界條件。當t≥tz=z(t,r)=L時,

q1為來自已干層頂部的熱量:
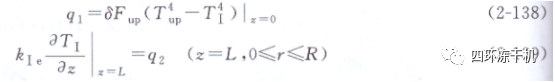
q2為來自擱板的熱量:
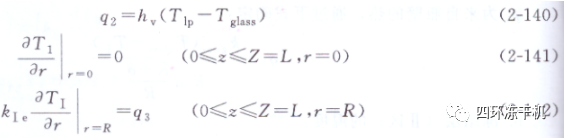
熱流q3為來自瓶壁的熱���,通過下式確定:

已干層中水蒸氣和性氣體的分壓: